数学で正射影ベクトルの求め方を忘れてしまったという方はいませんか?
そのような方は、きっとベクトル内積の意味がまるでわかっていないということでしょう。
今回はそのような方に向けて、ベクトル内積と正射影ベクトルの関係を示し、二度と忘れないように理解してもらいますので、最後までついてきてください。
ベクトル内積の意味
まず、ベクトルの内積とはなんでしょうか。
ベクトル内積の定義式を以下に示します。
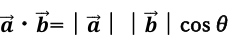
この式をそのまま暗記している方はいつまでたってもベクトルをうまく扱えるようになりません。
この式の正しい理解の仕方としては、まず│a→│cosθをセットで見ます。
│a→│cosθというのは、「a→の𝒃 →への正射影ベクトルの符号付き長さ」、つまりは下図において「c→の符号付き長さ」を示しています。
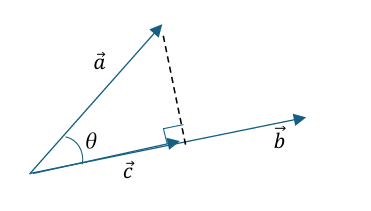
 牛タン
牛タン符号付き長さってなんだ?大きさとは違うのか??



いいところに気付いたね!符号付き長さってのは、ベクトルの大きさに向きの情報を符号として加えた値だよ。
ここで出てきた、「符号付き長さ」という単語を理解できれば、今回の内容はもうほとんど終わりです。
例えば、a→と𝒃 →がそれぞれ以下のような向きを向いていたとしましょう。


この図だと、c→はさっきと異なり、𝒃 →とは反対を向いていますよね。
この場合、「c→の符号付き長さ」は負の数になります。
まとめると、あるベクトルの符号付き長さというのは、そのベクトルの大きさに、向きに応じた符号をつけた値ということになります。
│a→│cosθが「a→の𝒃 →への正射影ベクトルの符号付き長さ」と書けることから、内積の定義は以下のように整理しなおせます。
a →・𝒃 →=│𝒃 →│×(a →の𝒃 →への正射影ベクトルの符号付き長さ)
このとらえ方、めちゃめちゃ重要なので、スラスラいえるようになってくださいね。
重要なのは、そもそも内積というのは正射影ベクトルを用いて定義されているという点です。
もっというと、内積をとるという操作は、あるベクトルから別のベクトルに正射影を下ろす操作とぴったりリンクしているともいえるでしょう。
ベクトル内積から正射影ベクトルを得る方法
それでは、本題の正射影ベクトルの求め方を考えてみましょう。
これは、先ほどの内積の定義が分かっていればごく自然に導くことができますので、公式など存在しません。
強いて言うなら、
符号付き長さ×単位ベクトル
でしょうか。
以下の問題を考えてみましょう。


この問題において、求めるベクトルを𝑥→とします。
先ほど勉強した内積の図形的意味を考えると、以下の順に演算すると正射影ベクトルが出てきますよね。
・(3,7)と(-1,3)の内積を取ると、𝑥→の符号付き長さと│(-1,3)│の積が出てくる。
・それを│(-1,3)│で割ると𝑥→の符号付き長さが出てくる。
・それを(-1,3)と同じ向きを向いた単位ベクトルにかけてあげると、𝑥→が出てくる。
これを式にすると以下のようになります。
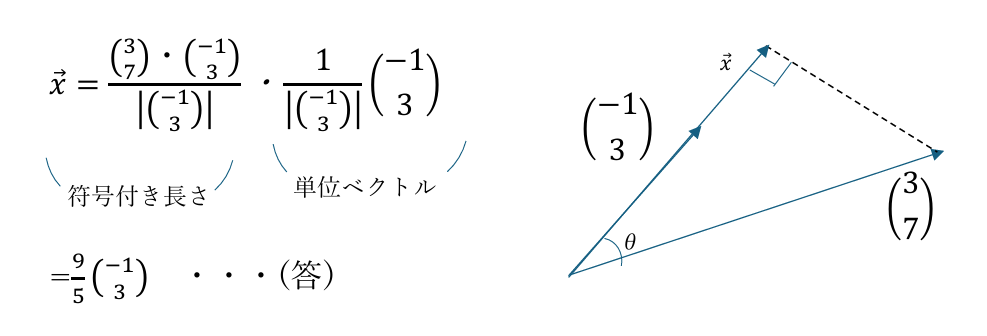
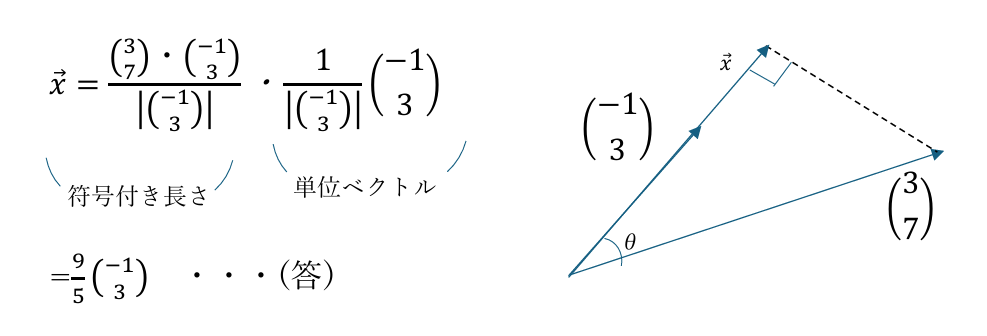
このように、内積の図形的意味を分かっていると、内積から正射影ベクトルの符号付き長さを作って、単位ベクトルにかけるという単純な操作で正射影ベクトルを求めることができます。
そして、「符号付き長さ」の便利な点が、二つのベクトルを具体的にイメージする必要は全くないことです。
二つのベクトルがどこを向いていたとしても、符号付き長さを求めた時点で向きの情報が勝手に式に含まれています。
例えば、a→とb→が以下のような向きを向いていたとすると、c→の符号付き長さは当然負の数をとりますよね。


これをb→の単位ベクトルにかけるので、c→は勝手にb→の反対向きのベクトルとして生成されるのです。
なので皆さんは脳死で符号付き長さを求めて単位ベクトルにかけるという操作をすれば良いことになります。
まとめ
ベクトルの正射影というのは、回転とならんで、ベクトルをうまく使いなすために最も重要な概念です。
正射影と回転をマスターすることにより、座標系において自由自在にベクトルを操れるようになり、図形の扱いが格段にうまくなります。
正射影についてもう一度ポイントを言うと、
・内積とはあるベクトルから別のベクトルに正射影を下ろす演算である
・この図形的意味を考えることにより、正射影ベクトルは自然に導かれる
ということをおさえておいてください。
回転については以下の記事を参考にどうぞ。




コメント