【受験数学】超絶便利なベクトル回転の方法。複素数平面などいらない！

ベクトルの回転させるというと、真っ先に複素数平面を持ち出そうとする人が多いでしょう。

しかし、回転ごときに毎回複素数平面を持ち出しては手間も時間もかかってしまいます。

今回はベクトルの正射影と並んで、ベクトルを自由に扱うための二大操作のひとつである「回転」について、サルでもわかるよに解説していきます。

↓ベクトルの正射影についてはこちら

ベクトルを回転させる3ステップ

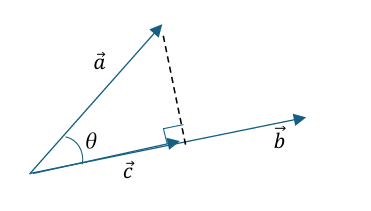
早速ですがあるベクトル(a,b)をθだけ回転左させたベクトルxを作ってみましょう。

ステップはたったの3ステップです。

これを式で表すと、以下のようになります。

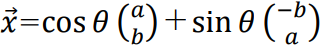
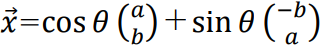
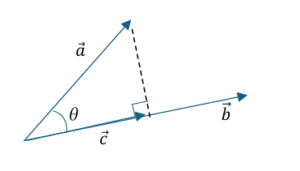
これだけだと分かりづらいと思うので、図にしてみました。

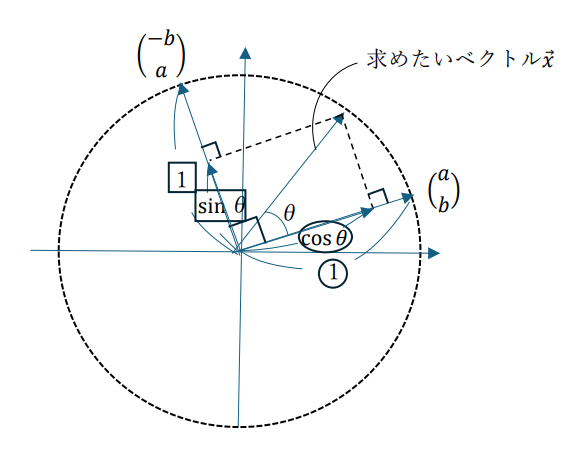
三角関数の定義さえ分かっていれば、あとはこの図を思い出すだけでベクトルを回転させることができます。

練習問題

それでは、いま勉強したベクトル回転を実際に使ってみましょう。

さっきのステップのとおりに考えてみましょう。

よって、求めるベクトルは、

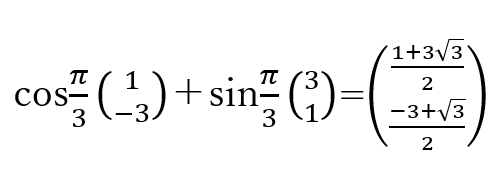
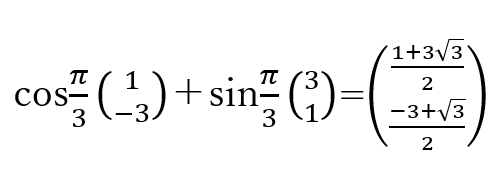
となります。

まとめ

いかがだったでしょうか。

冒頭でも言ったように、ベクトルは回転と正射影ができるだけで操作の自由度が格段に上がります。

座標系における図形の扱いがうまくなること間違いなしですので、必ずこの二つは当たり前に思えるように勉強しておいてください。

また、応用になるのでここでは書きませんでしたが、三角関数の加法定理も今回勉強したベクトルの回転を使って簡単に証明することができます。

こちらについては、公式LINEにご登録いただいた方に無料でプレゼントしている「ベクトルを自由に操る方法」にて詳しく解説しておりますので、以下のボタンからぜひチェックしてみてください。