東進の青木純二先生という先生をご存じですか?
「数学の神髄」という講座が有名かつかなりの評判で、東進では東大特進も担当している先生です。
私は同じく東進数学科の長岡恭史先生と、青木純二先生の授業を受けたことで数学の問題の見方が根本的に変わりました。
とてもおすすめな先生なので、この記事で授業の特徴について解説していこうと思います。
なお、説明に使用されている画像は当ブログオリジナル教材から引用しております。
初めて受けたらまじで目から鱗。
「数学の神髄」のすごいところ
論理の解説が秀逸

数学では本来、真か偽しかとらない「命題」や「条件」どうしを「∧(かつ)」「∨(または)」「→(ならば)」「¬(~でない)」という4つの論理演算子によって組み合わせて新しい「命題」「条件」を作った際に、その真偽がどうなるのかを考えます。
それぞれの論理演算子の定義は以下です。(AやBは個々の「命題」や「条件」を表しています。)
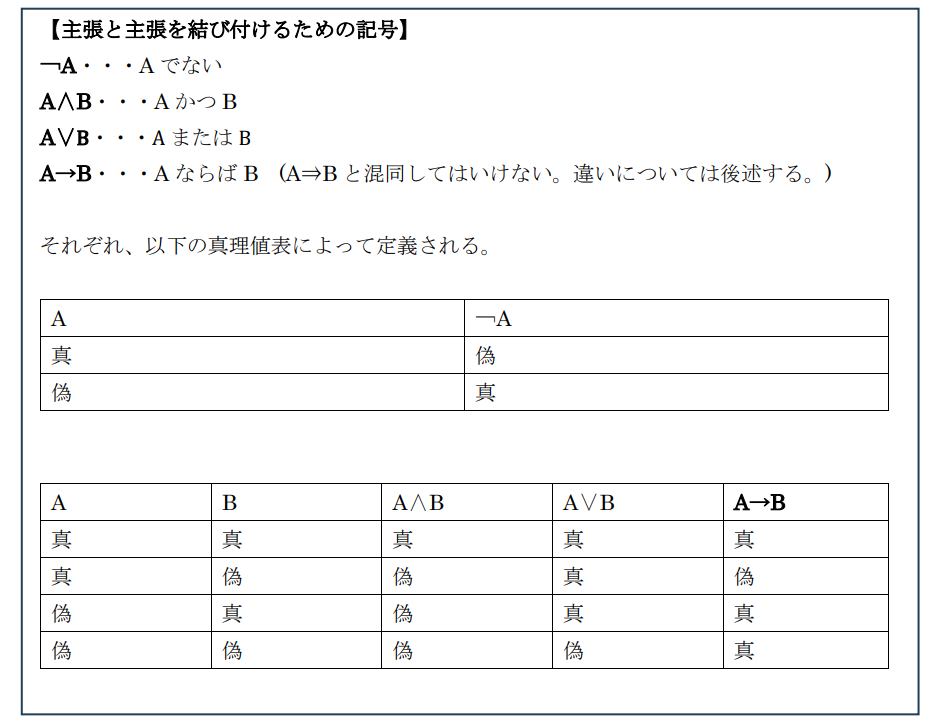
この考え方は数学の根本的なものであり、大学以降でも当たり前なのですが、学校や市販参考書でずさんに扱われているがゆえに意識できていない人が多く見られます。
私も授業を受けるまでは全く意識していませんでした。
最初はこのように問題を厳密に考えることが難しく思えるかもしれませんが、厳密であることは簡潔であることの裏表です。
厳密な数学の考え方を学ぶことにより、ごちゃごちゃと思考する必要がなくなり、難しい問題でもすっきりとした思考で解くことができるようになるのです。
考えるべき命題・条件を設定して正しく同値変形を行うという基礎の基礎を見直すことは、直接的な数学力の向上につながります。
この部分の解説が鬼ほど分かりやすいのが、青木先生の授業の一番の特徴です。
ベクトルの扱い方がうまい

ベクトルをベクトルの問題でしか使ったことがないという方、多いのではないでしょうか。
しかし実は、ベクトルは座標系においてとても応用の利くツールなのです。
ピンとこない人のために、ベクトルの基礎中の基礎である内積と回転について軽く説明します。
ベクトルにおいて最も重要な概念といえば、内積の図形的意味です。
【aとbの内積の図形的意味(アルファベット太字はベクトルを表す)】
a⋅b =│b│×(aのbへの正射影の符号付き長さ)=│b│×(下図cの符号付き長さ)
※a⋅b =|a||b|cosθとだけ覚えていてはダメ!
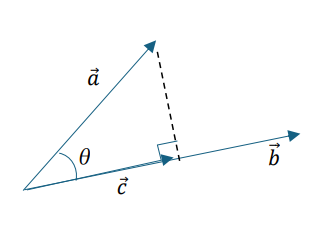
この理解ができると、正射影ベクトルを作れるようになります。
例えば、(3,7)の(-1,3)に対する正射影ベクトルは、
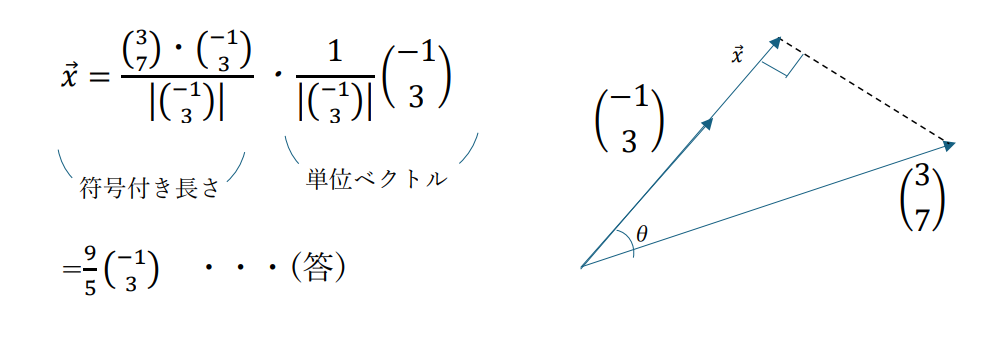
という感じで求めることができます。
なお、ベクトルの図が適当なのは、ベクトル内積の力によって勝手に答えが求まるので、いちいち図を想像する必要すらないからです。
また、あるベクトルは、法線ベクトルを用意することで好きな角度回転させることができます。
【ベクトルを回転させる方法】
ベクトル(a,b)をθだけ回転させたベクトルxは、
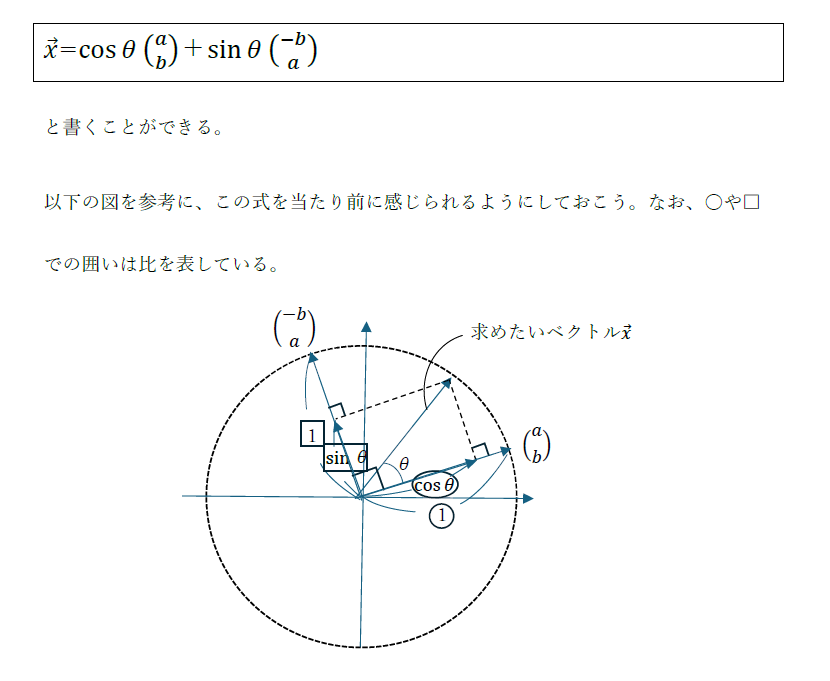
今回紹介した内積(正射影)と回転を使いこなし、ベクトルを自由自在に扱えるようになると、段違いで図形へのアプローチがしやすくなります。
青木先生の授業では図形をベクトルを用いて解釈して扱うことが多いので、ベクトルの理解が深まること間違いなしです。
参考書版「数学の神髄」
実は、青木先生は参考書版の「数学の神髄」も出されています。
問題を解く際のアプローチなどは授業の方が分かりやすいですが、金銭的都合などで授業を取りたくない方もこちらでエッセンスはつかめるかなと思います。
おわりに
青木先生の授業は、私が高校時代に受けた全ての授業の中でも、受けて良かった授業ナンバーワンです。
数学力がつくとは、「当たり前」が増えていくこと。
青木先生はそうおっしゃっています。
今まで暗記だけで数学を乗り切ってきた方も、青木先生の授業を受けて本物の数学力をつけ、公式を当たり前に思えるような勉強をしていくと、より合格が近づくのではないかと思います。
資料請求だけなら無料ですので、ぜひチェックしてみてください。
講師紹介映像(公式)
どんな先生なのか気になった方のために、公式が出している紹介映像を貼っておきます。参考にどうぞ。
LINE公式アカウントのご紹介
当ブログのLINE公式アカウントでは、受験生の方にとって有用な情報を定期的に発信しております。
現在、登録してくださった方には当ブログのオリジナル教材「数学の論理」を無料でプレゼントさせていただいています。
40ページ以上の少し長めの教材ですが、教科書には載っていない必須級の情報を詰め込んだ教材なので、ぜひ最後まで目を通してみてください。(教材の詳しい説明はこちら)
LINE公式アカウントのご登録は以下のボタンからお願いいたします。







コメント